 [German]It seems that a couple of Windows 10 users are facing system restore error 0x80070091. I've blogged about that issue within my German blog, and it seems that my solution works. Here are a few hints for my English readers how to analyze and solve this issue.
[German]It seems that a couple of Windows 10 users are facing system restore error 0x80070091. I've blogged about that issue within my German blog, and it seems that my solution works. Here are a few hints for my English readers how to analyze and solve this issue.
Advertising
I found several forum posts from December 2016 and January 2017 mentions this error code (see here, here, here, here, here for Windows 10, and here for Windows 8). But I came across this error the first time within a German Microsoft Answers forum post. A user describes the the error message as follows:
Version 1607 (Build 14986.1001)
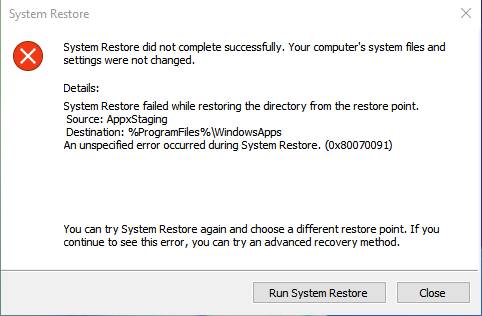
I'm using system restore to create a restore point. Then I tried to revert back to this system restore point. After a while I got an error 0x80070091.System Restore did not complete successfully. Your computer's system files and settings wern not changed.
Details: System Restore failed whil restoring the directory from the restore point.
Source: AppxStaging
Destination: %ProgramFiles%\WindowsApps
So system restore failed with error 0x80070091 due to something broken in AppxStaging. Below is also a screenshot detailing this error.
Error code 0x80070091 stands for ERROR_DIR_NOT_EMPTY (The directory isn't empty). Obviously something is broken in folder
%ProgramFiles%\WindowsApps
Advertising
so the AppxStaging function drops an error and refuse to rewrite the folder from system restore.
What's WindowsApps?
Windows 8 and later versions are using folder %ProgramFiles%\WindowsApps to store preinstalled apps Also Windows 10 is using this folder to store preinstalled apps.

The screenshot shown above list the subfolders used to store apps. There are also folders named Deleted or DeletedAllUserPackages or MovedPackages containing also entries. I guess, something during deleting, updating or moving an app went wrong, and a folder isn't left empty. Then AppxStaging isn't able to restore the app folder from system restore and drops an error. Maybe third party tools like antivirus software is blocking, but I don't know for sure. The best, what we can do: Try to proceed the following steps – beginning with simple approaches.
Feedback from my German reader of this blog post Windows 10 Version 1607: Unbekannter Fehler 0x80070091 confirms, that some solution works.
Addendum: How to list the WindowsApps folder as Administrator
Some user comments I received from my German blog post are indicating, that the folder
%ProgramFiles%\WindowsApps
contains some redirections (subfolders VFS with NTFS links) and could not be deleted. Virtual File System is used by App-V to redirect folders for instance. Perhaps something went wrong during updating apps. Robert Aldwinckle has suggested at Microsoft Answers forum a solution to list the folder's content without changing the permissions or tampering with TrustedInstaller rights. Here are the steps to proceed.
- Press Windows+X and select Command prompt (Admin), and confirm UAC (see Windows 10: Open command prompt window as administrator).
- Enter PowerShell in command prompt window and press the enter key .
- If the PowerShell command prompt PS C:\WINDOWS\system32> is visible, use the commands below.
The command below changes the path to folder WindowsApps.
cd $env:programfiles\WindowsApps
Then use the following command to enlist all sub-folders and its content via PowerShell and store the results within clipboard.
(LS -Re -Fi * -Fo -Ea:Inquire).FullName | clip

Then launch notepad using the PowerShell command notepad and insert the clipboard content pressing Strg+V. Afterward you can inspect all sub-folders within Windows editor. Search for VFS sub-folders for instance. My suspicion is, that some re-direction could be the cause for the system restore issue.
Fix #1: Try to remove third party tools and check your system
If a third party antivirus software causes this issue, the most simple approach is, to uninstall this AV software and use a vendor's clean tool to remove also files and settings remaining from uninstalling.
Reboot Windows and check the system for damaged system components, using the advices given within my blog post Check and repair Windows system files and component store. Also try to do a disk check for Windows drive (right click Windows drive, select Properties and use the Tools tab to start a disk scan).
Fix #2: Try system restore from Windows PE
If third party tools blocks system restore, maybe it helps to execute system restore from Windows PE. Just click the On/off button in start menu and select the Restart command while the Shift key has been pressed.
If the Windows PE shows the page Chose an option click Troubleshoot and go to Advanced options in the next page.
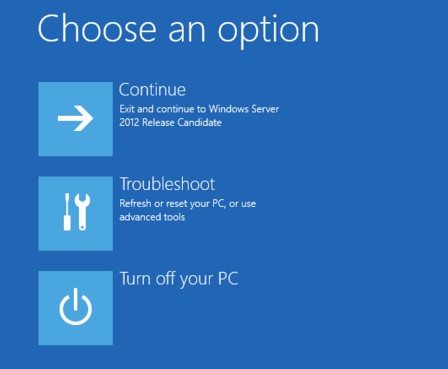
Within the Advanced options page select the System Restore tile and let Windows PE try to execute the system restore (see also Windows 10 hangs with error code 0xc0000034 or Windows 10: Defender Offline Scan boot loop – Part 2).

If it goes well, system restore is successful and your machine will revert to the selected restore point.
This approach has been discussed here and within the neosmart.net Wiki – but I fear, it won't help in many cases.
I read also, that renaming folder WindowsApps is possible within Windows PE (in command prompt window) without further hassle. The other solution is discussed below at Fix #5.
Fix #3: Synchronize Computer settings
There is another proposal how to fix system restore error 0x80070091 with synchronizing Windows settings. I found it within this MS Answers forum post.
- Go to Settings app (via start menu), click on Accounts
- Select Sync your settings
- Turn off Sync settings
Then reboot Windows and check whether system restore is back in operation again. But I fear, it won't help.
Fix #4: Uninstall Windows Apps
My idea was, to clean folder %ProgramFiles%\WindowsApps, because it is named as a root cause. One attempt could be to go to Settings app, select System – Apps & Features and try to uninstall all apps. But Windows 10 won't let you uninstall all pre-installed apps. So this attempt will fail.
It's possible, to use the approach discussed within this SuperUser thread, and remove all apps via PowerShell. But that probably didn't help, if the app causing the system restore error has been partly removed. Maybe disk cleaning (via Windows drive's property page) helps, but I'm skeptical.
Fix #5: Rename/clean WindowsApps folder
If you have proceeded the steps given above, and your are not successful at all, you run out of "simple click solutions". Then it's time for a more radical approach. We are going now to clean up the folder %ProgramFiles%\WindowsApps that is causing trouble.
Warning: You are at your own risk, and accessing this protected folder is a bit tricky – but feedback from my German blog readers say it works.
The biggest problem is to access the folder %ProgramFiles%\WindowsApps, because this folder is owned by TrustedInstaller and is protected in a special manner. So you are not even able to open this folder within Windows Explorer.
You can try to obtain the ownership of this folder, following the advices given here How to Get Access to WindowsApps Folder in Windows 10 or here or here. But I won't recommend this solution, due to the risk of unknown side effects – and because I have a more smart solution.
This blog post How to clean up the app folder in Windows 8.1 and 10 (delete app´s)! discusses how to use file manager Q-DIR to access the folder %ProgramFiles%\WindowsApps. I've used another approach: I executed the third party file manager Explorer++ portable within the Trusted Installer's context. Trusted Intaller has full access rights to %ProgramFiles%\WindowsApps.
The steps, how to launch Explorer++ portable with Trusted Installer credentials has been discussed within my blog post Windows 10: Execute programs as System/ Trusted Installer. Using this approach, enables me to create a copy of WindowsApps, inspect sub folders and subsequently delete entries.
- In a first approach just rename the folder WindowsApps to WindowsApps.old, using the approach outlined above.
- Then reboot your Windows 10 machine and try to execute system restore and let it restore a previous state.
Some users of my German blog post confirmed, that this solution worked. One user mentioned, that some VFS subfolders contains NTFS links (for folder redirections) and couln't be deleted, but the WindowsApps folder was renameable. System restore set the machine to a previous state, and all apps are also back. If that didn't cure the isse, your are able, to re-rename WindowsApps.old back to WindowsApps and try other fixes.
In case, you are not able to use process hacker and my solution above, or in case some files are locked, try to boot into Windows PE (see Fix #2) and go to the command prompt windows. Then try to enter the following commands (press enter key to execute each command):
cd 'C:\Program Files'
takeown /f WindowsApps /r /d Y
icacls WindowsApps /grant "%USERDOMAIN%\%USERNAME%":(F) /t
attrib WindowsApps -h
rename WindowsApps WindowsApps.old
Note: I assumed, that logical drive C: is the Windows partition. Please check, if that's true – sometimes Windows drive is D: (tip: you can launch notepad.exe and select File – Open to use Open dialog as a mini file manager). Drive X: is wrong, because this is Windows PE running in a RAM disk. I've added the attrib command due to GregoryLivingston's MS answers hint, that rename fails, if the folder is hidden. If the rename command fails, or if you like to delete the folder, use the command:
rd /s WindowsApps
The rd command deletes the WindowsApps folder with all sub folders. It's confirmed within this forum post, that the command sequence has worked. Then close command prompt windows and try system restore again. It should work now (if not, try a reboot first).
If fix #5 fails also, it's time to reset your Windows 10 to factory settings, using the Settings app. Hope, the hints given above helps to cure Windows 10 system restore error 0x80070091. Comments and further suggestions are welcome. If it worked for you, please let us know.
PostScript: There are indications, that the error could be related to January 2017 update for Windows 10. I've had a test machine with no other software installed, that fails with system restore error 0x80070091. But uninstalling KB3213986 won't cure this (see my comment within the [German] blog post) – you need to process the instruction of fix #5.
Addendum: Well, we have nailed it down to KB3213986 (see Windows 10 Update KB3213986 kills system restore).
Addendum 2: See my new findings here Windows 10: News about System restore error 0x80070091.
Similar articles:
Win10 Wiki
Windows: How to decode update 0x8024…. errors
Windows 10: Open command prompt window as administrator
Check and repair Windows system files and component store
How to fix Windows-Setup Hard Disk locked error
Windows 10: Defender Offline Scan boot loop – Part 2
Process Monitor: How to enable Windows 10 boot logging
Windows 10: Execute programs as System/TrustedInstaller







Thank you very much!
"Fix #5" solved my problem.
Hey, i have this restore problem and I think it's because I changed the permissions of WindowsApp a while ago:
http://image.prntscr.com/image/4333c6a650fa4299897e7dffcc50e280.png
So basicaly, what you recommend not to do.
What should I do?
It seems, that the issue is caused from Windows 10 itself. I just bootet a test machine with online Windows 10 V1607 installed since last summer. It has the restore error – I suppose, cumulative Update from January 2017 has something to do (although uninstalling this update didn't cure the issue).
Thanks for this great post. #5 fails as explorer++ says windowsapps is being used by other processes. Searching for file handles in processhacker, it's explorer.exe and skypehost.exe. Both can't be 'killed'. They both restart right away.
To clarify, I tried to rename
Hm, that's odd. Even, because explorer.exe doesn't have access right to this folder by default. Did you changed something?
Did you tried a clean boot (press shift key during selecting "restart").
What you can try, is Process Lasso, to kill thouse processes. Or try unlocker. I've never observed this behavior.
Another solution: Boot into Windows PE, obtain ownership and try to rename the folder – see the lengthy discussion here an Gregory Livingstone's post. See also my addendum to fix #5 above.
Thank you very much for the quick reply and suggestions.
I looked the file handles opened by explorer. It was xbox something. I used GeekUninstaller mentioned in option #4 to uninstall xbox apps and also skype app from windows store(which is in windowsapps). Then I could rename. Perhaps the rename is not even required as long as there is nothing using handles from windowsapps dir?
After that, I was able to successfully restore. Much thanks again for this detailed post.
I discovered the same problem, but solved it.
After killing explorer and skypehost, I found them in a process named background…
I killed these processes too, and was able to rename WindowsApps folder.
Hope restore will work now.
My system restore worked after renaming WindowApps.
Renaming it is difficult :
1. Need the right ownership and permissions (as documented elsewhere)
AND
2. Must kill all processes having this folder open.
– Explorer running in background
– Skypehost
I found these thanks to using ProcessExplorer….
Was very surprised about that
I dont get it how do u kill Explorer then renaming it. Can someone pls make a video for this??
Nvm problem sovled!
I use geekUninstaller and processExplorer
Just had to kill whatever was in the Windowsapp folder with processExplorer thanks for the help!
Hey can you tell how you did that via process explorer?
Pour moi aussi la solution numéro 5 a fonctionné chez moi, une fois la restauration du système effectuée, je n'ai plus eu de message d'erreur à l'ouverture d'un fichier EXE.
Merci beaucoup, ça m'a évité de devoir tout réinstaller.
I have this issue and I've followed Fix #5 but it states
"The system cannot find the file specified"
Any ideas?
Use dir to check whether the files/folders are available/visible. Also note the addendum within the commands in above text. The folder needs to made be visible with attrib, because it's hidden.
And I've had a typo in the first version of the folder name of the rename command (the s was missing).
The C: drive in system restore PE is a system reserved drive.
Your C: drive should be D: in the system restore.
Try navigate to D: and see list using command Dir. U will see your C: files in there.
Where exactly are the steps on how to use exploree++ to rename the windowsapp because in the link you mentioned i.e Execute programs… only process hacker is used.
I don;t think that i am supposed just to open explorer++ and rename the folder because that doesn't work either it needs trustedinstaller permission.
Thanks in advance
If you use the advise given in my linked blog post http://borncity.com/win/2017/02/22/windows-10-execute-programs-as-systemtrustedinstaller/ using process hacker to launch explorer++, it runs with truested installer privileges. Then you can use the context menu command Rename to change the folder name.
As an alternative you may use the commands given above in Windows PE to rename the folder.
Thank you for the info. I came to this page after posting the problem (https://answers.microsoft.com/en-us/windows/forum/windows_10-files/unable-to-enter-text-into-search-box-missing-tile/82dd6c8d-a552-40a5-814b-05aa7d6f4af3) I had. The only successfull solution was #5 but only at command line level; just glad I've done alittle of that in the past and for detailed guidance.
The restore process took nearly one hour to complete and then reported that the restore had error (something like) 0x8000ffff. Hit the finish button PC restarted and came up with message that the restore was successful.
PC does seem to be working OK – but somewhat slower and I do seem to have lost a few links on the browser (Firefox).
The error code 0x8000ffff stands for E_UNEXPECTED – an unexspected error.
https://answers.microsoft.com/tr-tr/windows/forum/windows_7/sistem-geri-y%C3%BCkleme-hatas%C4%B1/305742c8-1183-4f0b-9809-672958f8effe?rtAction=1488549025545 burdan bakın
That doesn't help.
I had this problem yesterday. I tried everything what has been described here, and only the System Image Recovery worked out for me. (Lucky, I had a fresh one ;)
Renaming the folder %ProgramFiles%\WindowsApps did the trick!
I used Hirens Boot CD to change the name of this folder, then restarted the PC and now System Restore works fine again. Thank you very much
I have tried the #5 option, but am running into an issue. I downloaded Process Hacker, plugins, etc. When I try to click "Run as Trusted Installer.." in Process Hacker it says "This option requires elevation." Did I do something wrong?
Disregard the above comment. I forgot to Run as Administrator. However, I am getting an error after running Explorer++ in Trusted Installer. When I try to change the name of WindowsApps, it says "The action can't be completed because the folder or a file in it is in use in another program". I don't know how that is possible.
Some reader came back with such a comment, mentions some apps like skype. There are some solutions to overcome this issue:
* Try to identify the apps in Task-manager and uninstall the blocking apps (one reader did that)
* Try to use a tool like unlocker (no idea whether that fits)
* Boot into Windows PE (not safe mode) and use the command prompt windows to overtake ownership and rename/remove that folder.
The last approach is mentioned within the above text. Hope that helps.
I know that i am stupid but when i type the 1st command in windows RE and hit the enter it gives an error saying the file cannot be found by the system….dafuq? ? Oh and thabks again for your time
Ok no need to answer i used process hacker and it worked like a charm….tahnks a looooooooooot
Due to the issue I was trying to fix via system restore, I cannot access windows explorer and so am limited to fix #5. However, when I try to enter the second command (takeown /f WindowsApps /r /d y) the system tells me "ERROR: The system cannot find the file specified"
How do I make the folder visible within command prompt? Please explain like I know nothing.
Thanks
Be sure, that C: is the Windows partition – on some system it's D:
I have Piriform Defraggler. Somehow, I was able to search on "windowsapps", and Defraggler came up with two filenames – names are simply "[Folder Entry]". I right-clicked on one, –> Open containing folder –> clicked 'Continue' for "You don't currently have permission to access this folder" –> clicked "security tab" to 'gain access to this folder' –> clicked 'Advanced' under the 'Security' tab on the "Windowsapps Properties" pop-up –> forgot what I clicked to get to the big long name of a file that ended with \windowsapps, which showed the owner was "TrustedInstaller", which I could change –> clicked "Object Types" and selected User, then clicked "Advanced" –> 'Find now" –> selected myself –> ok, ok, ok. Went back to Defraggler, right clicked on the file, and now I can get into them. Can also delete at least one. Not sure what I'm supposed to do now, but at least I got access this way. Am I on the right track?
http://h30434.www3.hp.com/t5/Notebook-Operating-System-and-Recovery/C-Windows-WinSxS-Temp-PendingRenames/td-p/3183223
I have some of these. Maybe helps explain something?
I did fix #5, yet now after I did the system resyore, I got an error 0x80070005. Anybody who could help me with that?
0x80070005. access denied. Do you use a third party antivirus software?
Pingback: PC upgrades Part 2 – Yuriy Baldyasov
I'm having a problem with step #5. In the cmd I'm "Administrator: X:\windows\system32" and after step 1 (I had to use D: instead of C: because it couldn't find C:) I'm "X:\Program Files" running command 2 brings up: ERROR: the system cannot find the file specified.
Using Dir command tells me I have 0 files and 3 dirs. The dirs were forward, backward, (represented as . And .. respectively.) and Common files. Exploring common didn't help. Can anyone help?
If you are still on "X:\Program Files" – you try to change Windows PE running in RAM disk. There is something like "D:\Program Files" required.
My C:\ program files worked but second command is giving me the same error
I solved the System Restore problem with solution #5 using Windows PE. However :
(A) In the first command (CD) I used D: rather than C:, even though it's C: in normal Windows.
(B) The ICACLS command gave an error message that finished with "no files processed". But this did not prevent the final RENAME command from working.
Hello,
Thanks for this tutorial…. Fix #5 worked, although I had to boot in "safe mode" to be able to rename Windowsapps. After that, I could restore the system to a point before that weird cumulative update from these days.
Olivier
PS: Why did I want to restore the system ?? Because after that update, I was unable to print on any of my printers ! A "test page" resulted in a message saying that the drivers were not installed. And nothing worked to install them !
Hello,
I tried to remove (or rename) WindowsApps, but when I entered the command on C:\WINDOWS\system32>rd /s WindowsApp, the following comment occurs:
WindowsApp, êtes-vous sûr (O/N) ? O
Le fichier spécifié est introuvable.
So should I give the right pass to the file, with no risk to delete all the specified files?
Thanks in advance.
Was able to rename windosapps dir.
Then restored to a ¨previous restorepoint.
After reboot PC again windows recovery loop.
Any suggestions ?
Try to boot in Windows PE – with a boot media – and try another recovery point.
Thx
I´ve 3 restorepoints; from 2 of them I can restore but then on both of them I get the recovery loop again.
On one (the last one before KB install) I get a restore error:
¨error in unpacking C:\windows\stsem32\AppVPublishing.dll¨
Also tried a trick (from the internet) with BCDEDIT :
BCDEDIT
You will see list of boot options with its {GUID} identifiers. Look for the one containing the line resumeobject.
bcdedit /set {GUID} recoveryenabled No
Did not help either.
Do not want to do a new install, because I´ve a lot of programs installed.
Do you have more suggestions ?
Hi
The hack of #5 worked perfectly for me. I used ubuntu bootable USB. In try mode ubuntu has perfec acces to al Windows folders. Renaming WindowsAps was not an issue. After that restore came with another error but system rebooted and restore was finished successfully. I think the hack with ubuntu is much better. It worked for me when recovering other crashes.
In addition to the same restore problem above, I can do an Export of the registry from the registry editor
regedit
but I then can't immediately Import in the registry editor that same file that I just exported.
In fact, using 3rd party apps such as Wise Registry Cleaner I can Backup the registry but I can't immediately restore that just backed up file.
I used to be able to do the above but sometime recently it started failing.
Fix #5 worked for me! Just had to modify it slightly…
Commands I Used:
cd 'D:\Program Files'
takeown /f WindowsApps /r /d Y
icacls WindowsApps /grant "%USERNAME%":(F) /t
attrib WindowsApps -h
rename WindowsApps WindowsApps.oldpieceofjunk
What's Different:
1): My files were in drive D instead of C
2): Had to modify the icacls command line because it failed at first, but after running "icacls /?" I learned that the %USERDOMAIN% portion wasn't ever asked for by icacls so I got rid of it and it ran without errors
3): I renamed WindowsApps to something that better matched my frustration by this point in the process. Let's just say I'm glad this is fixed lol
Thanks for the help and the suggestion to rename the WindowsApps folder!
Richard
Hey man second command isn't working. It's saying the system cannot find the file specified. What should I do?
The commands I used on Windows 10 [Version 10.0.14393] to successfully resolve the failed System restore 0x80070091 Error:
cd D:\Program Files
attrib WindowsApps -h
rename WindowsApps WindowsAppsOld
To clarify:
Windows 10 Enterprise Ver 1607
OS Build: 14393.1480
Fix #5 did the trick!
the icicles command failed, but I ignored it and went to attribute and the rename – it worked. I did have to reboot the system, going directly to running Win10 didn't work.
THANK YOU!!!!!
Hello GL,
Thank you for all the work you've done posting solutions to the Win10 System Restore failure.
Besides this issue, I've run into another issue with Win 10 that seems to relate to redirecting folders. After I partitioned the harddrive on my new laptop, I tried to make Windows store My Documents, My Music, My Videos and My Pictures on the newly created "data" E:\ drive. Now the OS is messed up. I'd be happy to give details about what I see.
Basically, I need a Windows expert to fix it for me since I'm not competent to that extent. Could you tell me where I might find a reputable expert on the Internet? I could give them remote access and, naturally, pay a fee.
Thank you.
Moving user profile folders isn't always a good idea! Microsoft doesn't support that in several scenarios (i.e. during feature upgrades), although they provided a path tab in folder settings to move user folders.
Thank you, GL. The user folders did get moved to E:\ but the OS itself is messed up. E.g., User Accounts on C:\ does not see me by name even though I log into my local account by name. Also, the Download folder on C:\ contains not only the few program downloads I have added (like Bitdefender and Paragon Partition Manager) but also most of the Windows files.
Thank you again for replying.
Thanks a lot !
#5 worked for me
The code I used
cd C:\Program Files
takeown /f WindowsApps /r /d Y
icacls WindowsApps /grant Administrator:(F) /t
attrib WindowsApps -h
rename WindowsApps WindowsApps.old
Hope it help for someone !
Hi guys Please I am trying to do step #5 but I get 'access denied' in my last line of code when I write 'rename WindowsApps WindowsApps.old'. Why am I getting Access denied? Please help I really need to do a system restore.
Thank you for this great post. #5 worked using explorer++. for me. I was able to rename the WindowsApps folder and carried out a system restore, successfully.
Thank you very much
Q-Dir saved me from reinstalling Windows10 anniversary. I can finally restore again but lost the Store in the process: No big deal as I used only 2 Store apps on a regular basis but when I click on a JPG image nothing happens now and I cannot change the file defaults linked to ex-Store apps. How to set Media Player as default for viewing pictures in Windows 10 1607? Is there a way to get the Store back without opening a second account or using ISO files, I am tired doing that since I upgraded from W7 to W10, repair same and always lose files, settings and my Office/Adobe subscriptions, just not worth it. I can list all the Windows default apps in PowerShell including the Store but cannot add anything (path c:\program files\windowsapps\xxxxx no found) that WindowsApps folder is now empty.